Sådan forenkles matematiske udtryk
Forfatter:
Monica Porter
Oprettelsesdato:
17 Marts 2021
Opdateringsdato:
17 Kan 2024
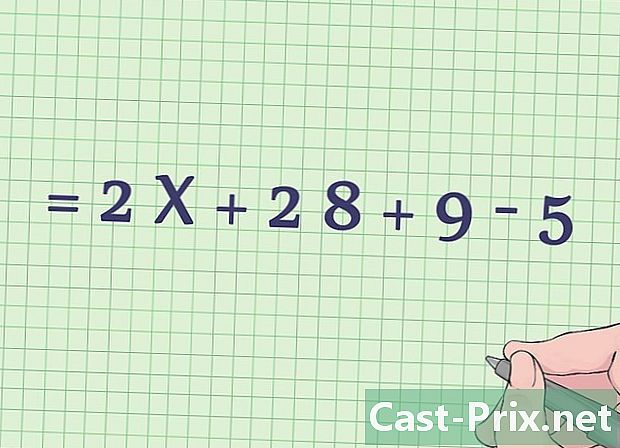
Indhold
I denne artikel: Respekter rækkefølgen af operationer Forenkle mere komplekse udtryk
Studerende bliver ofte bedt om at reducere matematiske udtryk "til deres enkleste form" - det er at forenkle det så meget som muligt. Uanset hvad der er groft eller forenklet forbliver udtrykket det samme, simpelthen i det andet tilfælde er det mere elegant og frem for alt lettere at håndtere. Undertiden betragtes øvelsen som "færdig", når udtrykket reduceres til det enkleste udtryk. Derfor er det vigtigt at vide, hvordan man reducerer et matematisk udtryk. Faktisk er det endda en næsten konstant operation. Men læs videre!
etaper
Metode 1 Respekter rækkefølgen af operationer
-

Lær rækkefølgen af operationer. Når man ønsker at forenkle et matematisk udtryk, fungerer man ikke idiotisk fra venstre mod højre, alt efter hvad der præsenterer sig selv. Nogle operationer har prioritet frem for andre og skal udføres først. Hvis du ikke følger denne ordre, får du ikke det rigtige resultat. Rækkefølgen af operationer er: parenteser, eksponenter, multiplikation, opdeling, tilføjelse og endelig subtraktion. Det er et mnemonisk middel til at bevare denne orden: tænk på "PEMDAS": "Fordi det siger Ma: Vent Simone!" (gratis at finde dig bedre!)- Det er dejligt at kende denne rækkefølge, og det er nyttigt til mange udtryk, men sommetider har du brug for mere komplekse teknikker til at forenkle, herunder polynomer. Se metode to for mere information.
-

Start med at behandle det, der er inden for parenteser. I matematik er disse der for at indikere, at deres indhold har prioritet frem for ethvert andet element. Denne prioritering er gyldig uanset hvilke operationer der er inde. På den anden side, men det er logisk, bruger parenteserne rækkefølgen af operationerne. Således skal vi først foretage multiplikationerne, derefter tilføjelserne osv.- For eksempel vil vi bruge udtrykket: 2x + 4 (5 + 2) + 3 - (3 + 4/2). Du skal først beregne alt inden for parenteser. 5 + 2 og 3 + 4/2, hvilket giver os 5 + 2 = 7 og 3 + 4/2 = 3 + 2 = 5.
- Den anden term i parenteser giver 5, fordi vi for det første dividerer 4 med 2. Hvis vi følger ordren for operationer, hvis vi tager ordet, som det kommer i rækkefølgen, foretager vi 3 + 4 og vi deler med 2, det vil sige at sige, at vi får 7/2: guld, det er forkert!
- Nota bene : Hvis der er en parentes i parentesen, starter vi altid med den indeni, og vi slutter med den på ydersiden.
- For eksempel vil vi bruge udtrykket: 2x + 4 (5 + 2) + 3 - (3 + 4/2). Du skal først beregne alt inden for parenteser. 5 + 2 og 3 + 4/2, hvilket giver os 5 + 2 = 7 og 3 + 4/2 = 3 + 2 = 5.
-

Lad os derefter gå til udstillere. Nu hvor vi har behandlet parenteserne, skal vi angribe eksponenterne (hvis der selvfølgelig er!) Et nummer med en eksponent er let at se: der er et tal (base) og øverst til højre, skrevet i mindre , eksponenten, også et tal. Foretag beregningerne separat, og erstatt derefter værdien med eksponenten med dens beregnede værdi.- Nu hvor vi har behandlet parenteserne, er vores udtryk nu: 2x + 4 (7) + 3 - 5. Den eneste term med en eksponent her er: 3, der er lig med 9. Vi erstatter udtrykket, og vi får: 2x + 4 (7) + 9 - 5.
-

Det er vendingen til multiplikationerne! Nu skal alle multiplikationsoperationer udføres. Multiplikationstegnet findes i forskellige former: symbolet ×, en prik, en stjerne eller endda intet overhovedet! således, 4 (y) er en multiplikation, det svarer til 4 x y- Der er to multiplikationer i vores øvelse: 2x (2x = 2 × x) og 4 (7). Da vi ikke kender værdien af x, forlader vi udtrykket som det er, dog 4 (7) = 4 × 7 = 28. Ligningen bliver derefter: 2x + 28 + 9 - 5.
-
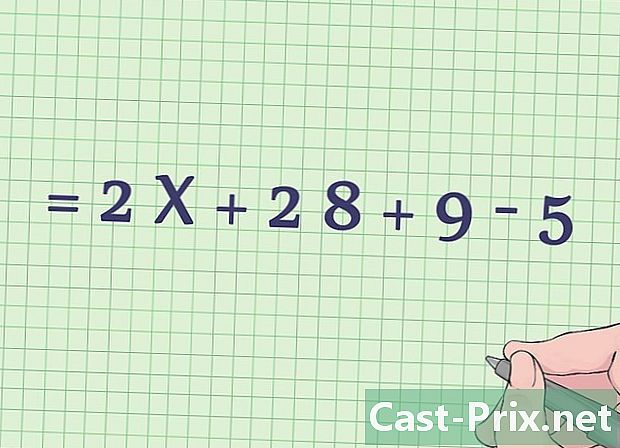
Lad os gå videre til divisionen. Ligesom tegnet om multiplikation kommer delingstegnet i forskellige former: symbolet ÷, men også skråstreget (/ eller "skråstreg", som i 3/4for eksempel - og den vandrette brøklinie.- I vores eksempel er der ingen opdeling (undtagen 4/2 set ovenfor), så vi springer over dette trin. Denne observation kræver en bemærkning: vi anvender PEMDAS-princippet i det omfang, operationen findes i dit udtryk, ellers går vi videre til den næste operation.
-

Derefter tilføjes. Det næste trin er at tilføje alt sammen. Vi kan selvfølgelig tilføje fra venstre til højre, men nogle gange kan vi gøre grupperinger. For eksempel med udtrykket 49 + 29 + 51 + 71 er det bedre at fremstille 49 + 51 = 100 og 29 + 71 = 100, hvilket giver: 100 + 100 = 200, snarere end 49 + 29 = 78, 78 + 51 = 129 og 129 + 71 = 200.- Som et resultat af PEMD-operationerne ligner vores udtryk: "2x + 28 + 9 - 5". Nu skal vi tilføje, hvad der skal være - tage tilføjelser, når de kommer fra venstre til højre. Du kan ikke tilføje 2x og 28, fordi der er en variabel (x kan ikke tilføjes, før du kender dens numeriske værdi). Hvad angår 28 + 9, giver dette 37. Hvis vi skriver om udtrykket igen, har vi: "2x + 37 - 5".
-

Træk. Det sidste trin i PEMDAS er subtraktion. Du skal kun have subtraktioner tilbage (men dette er ikke obligatorisk). Dette trin kunne have været udført tidligere, hvis vi overvejer at at trække fra er at tilføje et negativt tal. Disse to sidste operationer (tilføjelse og subtraktion) kan udskiftes.- Takket være PEMDA ser vores udtryk således ud: "2x + 37 - 5". Nu fratrækker vi, hvad vi kan. Vi kan trække 5 fra 32, hvilket er 32 - 5 = 32.
-

Kontroller dit udtryk en sidste gang. Normalt på dette tidspunkt reduceres dit udtryk til det maksimale. I det særlige tilfælde af ligninger med en ukendt (x) har du et reduceret udtryk, men ikke helt. Det vil være, når x tildeles en numerisk værdi. Det er dog også muligt at forenkle en ligning med ukendte (se nedenfor).- Der er taget hensyn til alle PEMDAS, det endelige svar er: "2x + 32". Man kan ikke forenkle yderligere, fordi 32 og 2x ikke kan tilføjes på grund af tilstedeværelsen af en variabel, 2x. Når vi kender værdien af x, kan vi afslutte beregningerne. Anerkender, at det stadig er mere praktisk end det originale udtryk! ekspression.
Metode 2 Forenkle mere komplekse udtryk
-

Tilføj de identiske ukendte. Hvis du har en ukendt i dit udtryk, skal du vide, at du kan tilføje eller trække identiske ukendte med den samme eksponent (eller "identiske udtryk"): det fungerer nøjagtigt med normale tal. Lad os gentage det: det ukendte skal være identisk, og eksponenten også! For eksempel kan 7x og 5x tilføje, men ikke 7x og 5x.- Denne regel gælder også for udtryk, der indeholder flere ukendte. For eksempel kan 2xy føjes til -3xy, men ikke til -3xy eller -3y.
- Lad os se nærmere på udtrykket: x + 3x + 6 - 8x. Her kan vi tilføje 3x og -8x, fordi de har den samme magt. Forenklet bliver udtrykket: x - 5x + 6.
-

Forenkle en brøkdel ved at dividere med eller "slette" almindelige faktorer. Fraktioner, der kun indeholder numeriske værdier (fravær af ukendte), både tæller og nævner, kan forenkles på forskellige måder. Første (måske den enkleste) metode: du deler tælleren direkte af nævneren. Hvis du har et produkt øverst og nederst i brøkdelen, og et af udtrykkene vises på begge sider, kan du desuden "forenkle", fordi de annullerer (deres opdeling er lig med 1). Så for at opsummere, hvis begge udtryk findes over og under brøklinjen, kan du slette begge dele.- Tag f.eks. Fraktionen 36/60. Hvis du har en lommeregner, skal du gøre opdelingen direkte, resultatet vil være: 0,6. Hvis du ikke har en, kan du slette de almindelige faktorer. For at gøre dette, opdel dine to numre i faktorer og se, om der er nogen fælles faktorer. 36/60 = (6 × 6) / (6 × 10), eller hvis du foretrækker: 6/6 × 6/10. Da 6/6 er lig med 1, bliver udtrykket 1 × 6/10 = 6/10. Det er ikke helt færdigt, da vi kan dele 6 og 10 med 2 3/5eller 0,6.
-
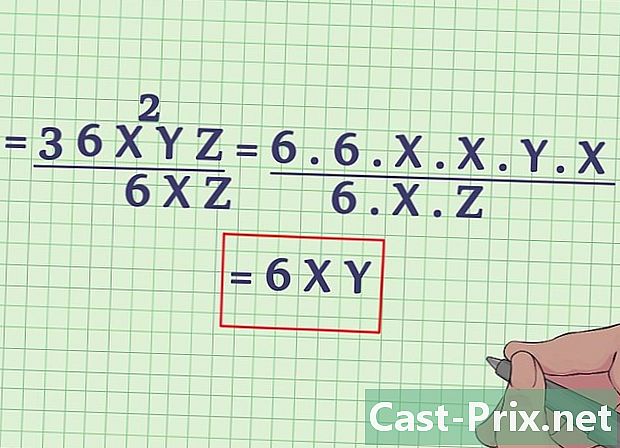
For fraktioner med ukendte er det det samme. Se, om der ikke er nogen udtryk (med en ukendt) fælles for begge dele af brøkdelen. Vi kan forenkle det ukendte med dets koefficient og eksponent.- Lad os tage udtrykket (3x + 3x) / (- 3x + 15x). Denne brøk kan skrives i formen: (x + 1) (3x) / (3x) (5 - x), 3x vises både i tæller og nævner, så vi kan fjerne det øverst og nederst. Derefter får vi: (x + 1) / (5 - x). Tilsvarende i udtrykket (2x + 4x + 6) / 2 kan alle udtryk deles med 2 Vi opnår derefter: (2 (x + 2x + 3)) / 2og videre: x + 2x + 3.
- Advarsel! denne forenkling fungerer kun, hvis man har et produkt af faktorer øverst, og ditto i bunden. For eksempel i udtrykket (x (x + 2)) / x kan vi forenkle med "x", hvilket giver os: (x + 2) / 1 = (x + 2). På den anden side kan vi med (x + 2) / x ikke gøre noget, fordi vi har en sum øverst og ikke et produkt. Det kan ikke forenkles i denne form: 2/1 = 2.
-

Udvikle eller faktor? I nogle tilfælde, når vi ønsker at forenkle, så bizarre som det lyder, er det bedre at udvikle sig end faktorisere. Der er ingen fastlagt regel. Det er kun med den vane, at vi ser, hvad der skal gøres, idet målet altid er at forenkle udtrykket.- Eksempelvis giver udtrykket 3 (x + 8), når det udvides,: 3x + 24, mens 3x + 24x kan fabrikeres, og det giver: 3x (x + 8).
- I nogle tilfælde er det bedre at holde faktoren konstant foran et udtryk i parentes. Faktisk kan det bringes til at forsvinde. Det er nytteløst at udvikle sig for tidligt, forenkling er altid muligt. I fraktionen (3 (x + 8)) / 3x, for eksempel, er 3 til stede i tælleren og nævneren, så vi kan undertrykke det, hvilket giver: (x + 8) / x. Det er stadig lettere at håndtere end (3x + 24x) / 3x, resultat, vi ville have opnået, hvis vi havde udviklet alt.
-

Forenkle ved factoring. Factoring er en teknik, der kan forenkle en brøkdel ved undertiden at fjerne polynomer. Factoring er det modsatte af at udvikle sig. Et langt udtryk, en sum generelt, omdannes til et kortere udtryk, der er et produkt af faktorer. Denne faktorisering bør kun ske, hvis der bagved er en forenkling (som i en brøkdel). I nogle tilfælde (oftest med anden grads ligninger) gør factoring det også muligt at finde rødderne af ligningen hurtigere og lettere.- Lad os tage udtrykket x - 5x + 6. igen. Dette udtryk kan indregnes i (x - 3) (x - 2). Så hvis senere findes x - 5x + 6 i tælleren for en brøk, og hvis vi havde (x - 2) i nævneren, kunne vi så forenkle med dette udtryk. Eksempel: vi er nødt til at forenkle (x - 5x + 6) / (2 (x - 2)). Vi faktorer først tælleren, og derefter forenkler vi. Med andre ord ender vi med (x - 3) (x - 2) / (2 (x - 2)), vi forenkler med (x - 2) og vi får: (x - 3) / 2.
- Som nævnt ovenfor er der undertiden andre grunde til factoring.Faktisk tjener denne manipulation til at forenkle, men det gør det også muligt at løse en ligning lettere, især hvis denne sidst er lig med 0. Tag f.eks. Ligningen x - 5x + 6 = 0. Hvis man faktoriserer, får man: x - 3) (x - 2) = 0. For at løse denne ligning er det tilstrækkeligt, at et af udtrykkene er lig med 0, da 0 gange x = 0. Derfor, 3 og 2 er løsningen.